Generalization & Scaling

So far, we have focused on n = 3 robots to keep the model and explanations concise. However, the Self-Sorting Robots specification is fully parameterized and can be scaled to any number of robots simply by changing the roboCountTotal value in the setup.

In this section, we explore what happens when we increase the number of robots — and the resulting complexity of the system’s state space.

Benchmark Preview: Self-Sorting Robots in Action

The following transition systems were automatically generated using BiGGer and GrGen.NET, modeling the state space of multiple robots performing a physical bubble-sort along the grid.

N = 3 Robots	N = 4 Robots	N = 5 Robots
Nodes: 78 Edges: 96 Time: 0.70 s	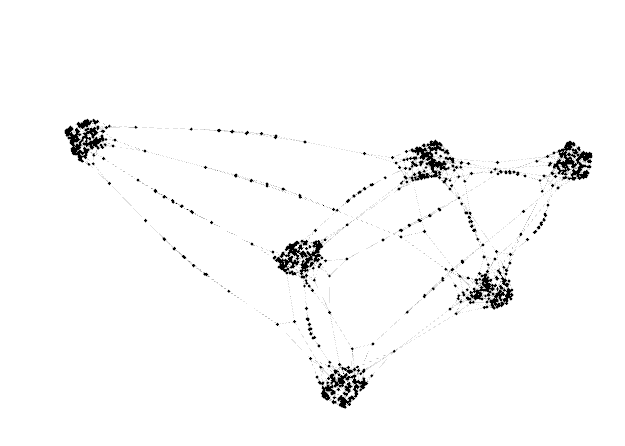Nodes: 1,263 Edges: 2,767 Time: 10.02 s	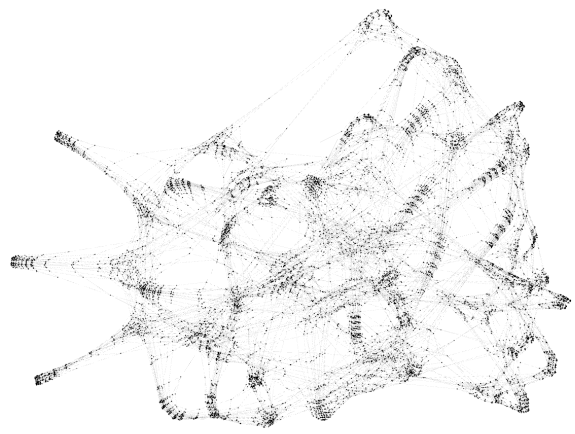Nodes: ≈ 9,192 Edges: 22,047 Time: 105.56 s

Interpretation:

• Each dot is a reachable system state.
• Each edge is a transition caused by applying a reaction rule.
• Larger N means many more possible configurations and paths.
• Graphs were rendered from .dot files using Gephi.

Observations

• The growth of the state space is combinatorial — adding just one more robot drastically increases the number of states and transitions.
• Execution time increases accordingly, even with optimized model-checking and parallel matching enabled.
• The structure of the graph often reveals sorting “phases” and possible deadlocks or cycles if rules are misconfigured.

Takeaway

Scaling SSR beyond small values of N is an excellent stress test for:

• Model checker performance
• Rule design correctness
• Visualization tooling for large graphs

It also shows the power of a single, parameterized bigraph specification to model a wide range of system sizes without rewriting the rules.